Distance variable improvement of time series in big data

 We will generate synthetic data of 3 random variables x1, x2, and x3 and we will evaluate y, the answer, by adding some noise to the linear combination. In order to frame the problem in a way where we can provide our big data models with the data as complete as possible, this python script will generate windows given a time series data,More info go through big data hadoop course

In the first place, let’s see what data we have and what therapy we are going to apply.

N = 600, —

Np.arange(0, N, 1).reshape(-1,1) t = t

t = np.array([t[i] + np.random.rand(1)/4 for I in range(len(t))])

T = np.array([t[i]-np.random.rand(1)/7 in the range(len(t))]) for I

Np.array(np.round(t, 2)) t =

Np.round((np.random.random(N) * 5).reshape(-1,1), 2) x1 =

Np.round((np.random.random(N) * 5).reshape(-1,1), 2) x2 =

Np.round((np.random.random(N) * 5).reshape(-1,1), 2) x3 =

N = np.round((np.random.random(N) * 2).reshape(-1,1), 2)

(y+n, 2) y = np.round

Then we have a “y” function, which is the answer and an additional noise of 3 independent random variables. The response is also directly correlated with the independent variables’ lags, and not just with their values at a given point. We ensure time dependence in this way, and we force our big data models to recognise this behaviour.

Also, the timestamps are not evenly spaced. In this way, we reinforce the idea that we want our big data models to consider time dependence, so they should not only handle the sequence with a number of observations (rows).

With the goal of inducing high non-linearities in the results, we included exponential and logarithmic operators in big data.

Big Data Windows framing

For all big data models of this work, the method followed is to reshape the information we have through fixed windows that will give the model the most complete information possible from the recent past at a given time point, in order to achieve an accurate prediction. In addition, we will check how the big data models are affected by providing previous values of the response itself as an independent variable.

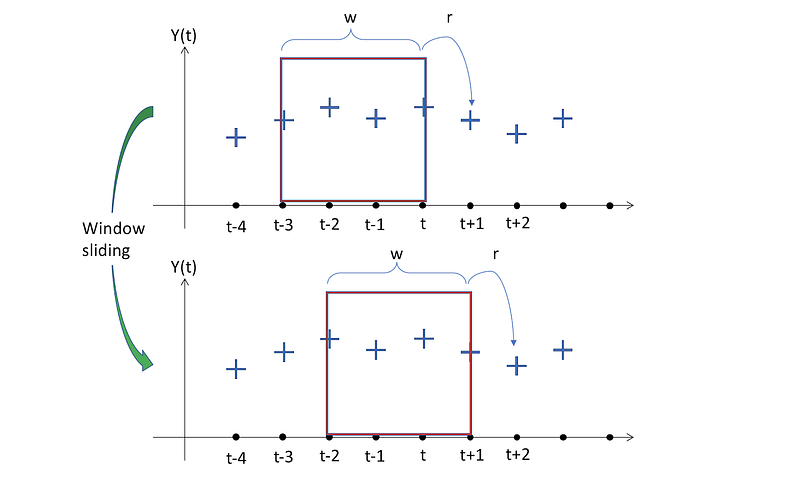
Let’s see how we’re going to make it happen.

Only the axes of time and response are shown in the image. Notice that there are 3 more variables in our case that are responsible for the values of “t”.

The image at the top shows the windows of a selected (and fixed) size w, which is 4 in this case. This implies that the model will map the data contained in those windows, with the prediction at t+1. There is an “r” in the response size since in the past we might want to estimate several time measures. This will be a friendship with many. We will function with r=1 for consistency and simpler visualization.

We can see the Sliding Window effect now. By moving the window one time step to the future, the next pair of input-outputs that the model will have for finding the mapping function is obtained and proceeds the same.

But first, we don’t want time to be absolute numbers, we are more interested in recognizing the time between observations that has passed (remember that the data is NOT spaced evenly!). Therefore, let’s build a ⁇ t and look at our information.

Dataset = pd. DataFrame(np.concatenate((t, x1, x2, x3, y), axis=1),

Column=[‘t ‘,’ x1 ‘,’ x2 ‘,’ x3 ‘,’ y ‘]))))

DeltaT = np.array([(dataset.t[i + 1]-dataset.t[i]) in the range(len(dataset)-1)])) for I

DeltaT = np.concatenate((np.array([0]), deltaT))

Dataset.insert(1, ‘alpha’, deltaT)

Head(3) dataset.head(3)

Now that we know how our dataset is going to look like that, let’s replicate what we want to do with our support feature over a table scheme.

For a size 4 window in big data models

All the information stored in the window, which is all the values inside the W window, and the timestamp(s) of when we want to make the prediction, will be flattened by our function.

That way, depending on whether we use previous values of the responses as new predictors, we may have 2 separate equations to model our method.

The result that must be returned by the function should look like.

We’re going to be able to build l = n-( w+r) +1 windows because the first rows are missing because we don’t have previous details for the first Y(0) value.

All the lags we listed function like new model predictors (the previous Y values are not included in this visualization, they will follow the same as the Xi. Then the timestamps (elapsed) where we want to make the prediction ⁇ t(4) and the corresponding value of what the prediction should be Y(4). Notice that as we want to standardize each window to be in the same range, all the first ⁇ t(0) is initialized to 0.

To accomplish this process, here is the code created.

Baseline Big data models for Creating Windows

The w = 5

TrainBuilder = WindowSlider)

Train-windows = train-builder.collect-windows(trainset.iloc[:,1:],,

Past-y = False)

WindowSlider) (test-constructor=

Test windows= test builder.collect windows(testset.iloc[:,1:],,]

Past-y = False)

WindowSlider) (train function Object() { [native code] } y inc=

Train-windows-and-inc = train-builder-and-inc.collect-windows(trainset.iloc[:,1:],

Past-y = True)

WindowSlider) (test function Object() { [native code] } y inc =

Test-windows-y-inc = test-builder-y-inc.collect-windows(testset.iloc[:,1:],,

previous y = True)

Windows.head train(3)

We can see how the windows carry in the history of the rest of the variables, the records of the (window-length) time steps, and the accumulative sum of ⁇ t. for each projection.

Prediction = Current

# Y pred = present Y

Cp.deepcopy(trainset) = bl trainset

Cp.deepcopy(testset) = bl testset

DataFrame(bl testset[‘y])) ‘bl y = pd.

Bl y pred = bl y.shift(periods=1)

Bl residuals= bl y pred-bl y pred

Bl rmse = np.sqrt(np.sum(np.power(bl residuals,2)) / len(bl residuals))

Print(‘RMSE = .2f percent ‘bl rmse percent)

Print(‘To train time = 0 seconds’)

# # RMSE = 11.28 = 11.28

To compare our coming results with, we already have a value. In view of my current value, we have applied the basic rule as the forecast. This approach can often unexpectedly work better than an ML algorithm for time series where the value of the answer is more constant (a.k.a stationary). The zig-zag of the big data is infamous in this case, leading to low predictive power.

Multiple Regression in Linear big data models

Our next strategy is to develop a multiple linear regression model.

MULTIPLE LINEAR REGRESSION #

Import LinearRegression from sklearn.linear model import

Lr model = LinearRegression)

Trainset.iloc[:,:-1], lr model.fit, trainset.iloc[:,-1])

(t0 = time.time))

Values of lr y = testset[‘y].

Lr y fit = lr model.predict(trainset.iloc[:,:-1])

Lr y pred = lr model.predict(testset.iloc[:,:-1])

The tF = time.time)

Lr residuals= lr y pred-lr y pred-lr yy

Now we have to beat a very strong model. With the new windows, the model seems to be able to find the connexion between the details of an entire window and the answer.

The Symbolic Regression in big data

Symbolic Regression is a type of regression analysis that looks for the model that best fits a given big data dataset in the space of mathematical expressions.

Genetic programming is the basis of symbolic regression and is thus an evolutionary algorithm (a.k.a. Genetic Algorithm-GA).

To summarise how the algorithm works in a few terms, we first need to understand that a mathematical expression, like the figure above, can be interpreted as a tree structure.

In this way, the algorithm begins with the first generation of a large population of trees that will be measured according to a fitness function, in our case the RMSE. The best individuals of each generation are then cross between them and even some mutations are added to include experimentation and randomness. When a stopping condition is met, these iterative algorithms terminate.

Conclusion

With almost a perfect fit in the validation results, we have seen that Symbolic Regression performs extremely well. Surprisingly, by including only the four easiest operators (addition, subtraction, multiplication, and division), with the disadvantage of more training time, I have achieved the best accuracy. I encourage you to try out various model parameters and develop the outcomes. You can learn more through Big Data Online Training